What is Haversine?
Haversine is a waveform that is sinusoidal in nature, but consists of a portion of a sine wave superimposed on another waveform. The input current waveform to a typical off-line power supply has the form of a haversine.
The haversine formula is used in electronics and other applications such as navigation. For example, it helps in finding out the distance between two points on a sphere.
The haversine is defines as a function of the sine for a particular angle θ by the formula Haversin (θ) = Sin2 (θ/2)
The conduction currents appear at the input of the rectifier as narrow positive and negative pulses. This is common with power supplies with large input capacitors. Since the capacitors are always charged at or near peak ac voltage for every cycle, the diodes will only conduct for a very short time. There diodes remain reverse biased most of the time since the capacitor voltage is higher than the AC input.
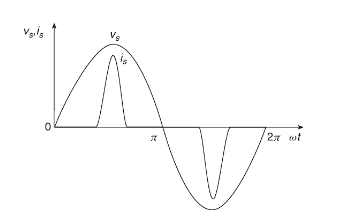
As such the input current waveform of such as power supply employing capacitive filter will therefore consist of haversine pulses, several harmonics, leading to a very low power factor. The diodes do not conduct throughout and are reverse biased most of the time. The relationship between the voltage and the unidirectional diode currents that flow during the conduction time is as shown in the waveform in figure 1 below.
Figure 1 Line voltage and current for a full wave peak rectifier Image Credit
The time period is equal to the conduction time of the diode and the current waveform looks like it has been chopped out of a vertically offset sine wave of that time period.
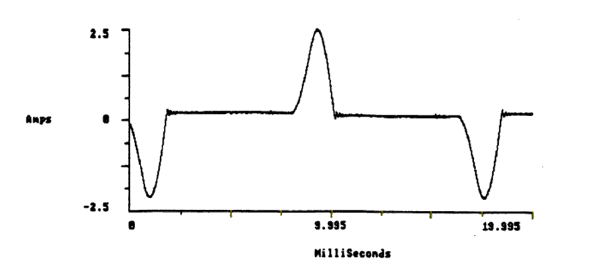
A typical non-linear current waveform in an SMPS is as shown in figure 2 below, this represent a haversine wave and was obtained using an oscilloscope together with a low inductance resistor.
It can be observed that waveform has unequal pulses, each with a different conduction time. In addition, the zero centers are offset. Since this is non-sinusoidal, the normal rms formula is not applicable. Instead, the Haversine formula is used to get the values of the pulses.
Figure 2 Haversine current pulse Image Credit
Calculating the true RMS value of a complex waveform such as that from the SMPS power supply is usually a challenge due to the non-uniformity of the wave. The wave containing pulses deviate from the traditional sine wave in which the RMS formula applies to.
One of the practical ways of establishing the true RMS value is by using digital sampling instruments. These have the ability to continuously sample the pulse and provide the value on its display. The other method, which is more accurate, is the use of an oscilloscope.